Алексей Толстиков, Михаил Шахрай, Глеб Гусев, Павел Сердюков
Yandex

АННОТАЦИЯ
В последние несколько лет много внимания уделялось вопросу оценки авторитетности веб-страницы на основе пользовательского поведения. Однако предложенные методы имели ряд недостатков. В частности, предложенные техники работали на единственном снимке графа сёрфинга, игнорируя его природную динамику с непрерывно изменяющейся пользовательской активностью, что приводит актуальность использования метода к нулю. В данной работе предлагается новый метод расчёта важности веб-страницы под названием Fresh BrowseRank. Оценка страницы нашим алгоритмом соответствует её весу в стационарном распределении гибкой модели случайного блуждания, которая управляется чувствительными к обновлениям весами вершин и рёбер. Наш метод обобщает некоторые ранние подходы, обладает расширенными возможностями для захвата динамики Сети и пользовательского поведения и преодолевает стандартные ограничения BrowseRank. Результаты эксперимента показывают, что наш подход способен генерировать более релевантные и более свежие результаты ранжирования по сравнению с классическим BrowseRank.

Категории и описание предмета: H.3.3 [Хранение и поиск информации]: Информационный поиск
Общая терминология: алгоритмы, опыт, показатели работы
Ключевые слова: авторитетность страницы, BrowseRank, новизна, поиск в сети, обучение

1. Введение
Оценка авторитетности веб-страницы является одной из самых важных характеристик, используемых алгоритмами ранжирования. Существует множество способов расчёт важности веб-страниц, среди которых есть такие алгоритмы, которые анализируют историю посещений пользователя. В частности, алгоритм BrowseRank [1] измеряет важность веб-страницы посредством расчёта её вероятности в стационарном распределении непрерывного процесса Маркова на графе сёрфинга пользователей. Несмотря на неоспоримые преимущества BrowseRank и его модификаций (см. раздел 2), эти алгоритмы не учитывают временную характеристику Сети. Более новые страницы, вероятно, более релевантны запросам, чувствительным к новизне, чем старые страницы и, как следствие, временная характеристика релевантности документа позволяет провести более чёткое разграничение между релевантными и нерелевантными документами. Учитывая существование регулярно обновляемых ресурсов, посвящённых новостям, политическим вопросам, спортивным обзорам или конференциям, пользователь, скорее всего, ищет информацию, относящуюся к самому последнему событию. По этой причине вопрос создания чувствительного к новизне (свежести, fresh) BrowseRank должен быть весьма актуален для поисковых систем.

Далее представлен алгоритм Fresh BrowseRank, который распределяет веса по страницам в зависимости от их новизны. Чтобы показать эффективность Fresh BrowseRank, мы сравниваем его с классическим BrowseRank на большой выборке в графе сёрфинга пользователей и демонстрируем, что наша методика имеет более высокую производительность по сравнению с оригиналом. Насколько нам известно, предложенный алгоритм является первым алгоритмом ранжирования, чувствительным к новизне и работающим на основе истории посещений пользователя.

Оставшаяся часть работы выглядит следующим образом. Раздел 2 содержит краткий обзор подходов к измерению важности страницы. В разделе 3 мы описываем структуру, которая помогает представить описываемый в работе алгоритм. Мы определяем, что такое FreshBrowseRankв разделе 4. В разделе 5 мы описываем метод, используемый нами для настройки параметров алгоритма. Результаты опыта описаны в разделе 6. В разделе 7 мы обсуждаем возможное применение и последующую работу.

2. Проделанная работа
Широко применяемым методом оценки важности веб-страниц является анализ сети в виде графа веб-страниц, соединённого гиперссылками. Наиболее известным представителем алгоритмов ссылочного анализа является PageRank (Page и др. [2]). Согласно алгоритму оценка страницы p равна её весу в стационарном распределении дискретного процесса Маркова, который моделирует случайное блуждание пользователя по гиперссылочному графу. Однако подобный метод оценки обладает рядом уязвимостей. В частности, значительная доля страниц и ссылок является ненадёжной и не используется реальными людьми. Прочие варианты используют качественно иной вид данных. Как следствие, моделирование случайного блуждания на плоском гиперссылочном графе не реалистично. В 2008 Liu и др. [1] предложили алгоритм BrowseRank, который рассчитывает важность веб-страницы, используя данные о поведении пользователей. Граф сёрфинга содержит множество информации, такой как время пребывания пользователей на странице, число переходов между веб-страницами и т.д. В отличие от PageRank, основанного на дискретной случайной работе, BrowseRank использует непрерывный процесс Маркова на основе статистики сёрфинга пользователей. Такая модель является более реалистичным подходом к оценке важности веб-страниц. Однако подходящий алгоритм ранжирования должен обладать некоторыми свойствами, которых нет у BrowseRank. Liu и др. в [3], [4] предложили разнообразные модификации алгоритма, которые позволяют устранить некоторые недостатки. В [3] показаны новые способы оценки распределения времени пребывания. В [4] используется Скелетные Процессы Маркова для моделирования случайного блуждания веб-сёрфера. Они показывают, что этот фреймворк охватывает множество существующих алгоритмов (среди которых PageRank, Usage-based PageRank [5], TrustRank [6], BrowseRank Plus, MobileRank [7] в качестве модификаций). Параметры этих алгоритмов могут выбираться таким образом, что они будут работать аналогично классическому BrowseRank. Существуют и другие подходы к вычислению важности веб-страницы с использованием данных о пользовательском поведении, которые не применяют модель случайного блуждания (например, [8]).

Важной проблемой, которая не решена ни одним из упомянутых алгоритмов, является проблема ранжирования новизны. Как показано в [9], граф сёрфинга существенно меняется каждый день. Поэтому страницы, имевшие высокий BrowseRank несколько дней назад, могут не быть авторитетными в настоящий момент.

Yu и др. [10] были первопроходцами в изучении алгоритмов ссылочного анализа, чувствительных к временным характеристикам Сети. Авторы модифицировали PageRank посредством взвешивания каждой гиперссылки в соответствии с её возрастом. Прочие алгоритмы ссылочного ранжирования, чувствительного к новизне, изучались Amitay и др. в [11], Berberich и др. в [12] и [13], Yang и др. в [14], Dai и Davison в [15]. Алгоритм T-Fresh из последней работы обобщает идеи из всех остальных вышеупомянутых публикаций. Однако T-Fresh обладает несколькими недостатками, которых нет в алгоритме APR за авторством Жуковского и др. в [16]. Оба метода основаны на взвешивании графа, которое собирает информацию о свежести страниц и гиперссылок. Dai и Davison вывели два новых фактора важности страницы, которые зависят от свежести самой станиц и свежести ссылок. В отличие от T-Fresh, оценка свежести APR зависит от скомбинированного поведения страниц и ссылок. Такой подход позволяет контролировать влияние обоих типов характеристик на назначаемую оценку. Следуя схожему принципу мы предлагаем методику решения проблемы нечувствительности BrowseRank к новизне, что показано в разделе 6. Насколько нам известно, в данной работе впервые рассматривается чувствительная к новизне разновидность BrowseRank.

3. Фреймворк и обозначения
Популярные поисковые системы постоянно предлагаю пользователям установить в их браузер свои тулбары, которые, помимо полезных возможностей отслеживают сессии пользователей, чтобы использовать собранную информацию для улучшения качества поиска. Анонимная информация, описывающая пользовательское поведение (посещённые страницы, количество посещений, поданные запросы и т.д.) сохраняется в логе браузера. Мы определяем сессии и граф сёрфинга пользователей аналогично Liu и др [1]. Пусть S — это сессия пользователя. Страницами сессии будут p1(S),p2(S),…,pk(s)(S). Для каждого i ∈ {1,2,…,k(S) — 1} тулбар делает запись pi(S) → pi+1(S). Мы называем страницы pi(S), pi+1(S) соседними элементами сессии S.

Для каждой страницы p из лога браузинга мы определяем число сессий, начатых с этой страницы как s(p). Для каждой пары соседних элементов {pi,pi+1} в сессии мы определяем число сессий, содержащих такую пару как I(pi,pi+1).

Мы определяем граф сёрфинга пользователя G = (V,E) таким образом: ряд вершин V состоит из всех веб-страниц, упомянутых в логе, а так же из дополнительной вершины x. Набор ориентированных рёбер E содержит все упорядоченные пары соседних элементов {p1,p2}. Так же он содержит дополнительные рёбра от последних страниц всех сессий к вершине x. Пусть σ(x) = 0. Для каждой страницы p при условии p → x ∈ E определим число сессий, завершившихся на p как I(p,x).

Освежим в памяти определение BrowseRank. Вероятность сброса σ(p) — это вероятность выбора страницы p при старте новой сессии. Она пропорциональна числу сессий s(p), начинающихся со страницы p. Поэтому σ(x) = 0. Вероятность перехода w(p1 → p2) — это вероятность клика гиперссылки p1→p2. Она равна I(p1,p2)/(∑pi → p ∈ E).

Оцениваемое время пребывания Q(p) страницы p определено в [1]. BrowseRank p равен Q(p)π(p), где

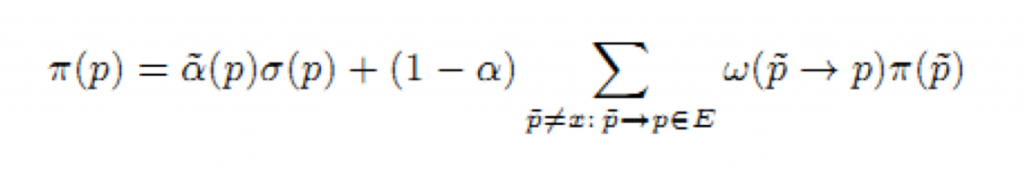(последние уравнения работают и при p = x), α_(p) = α(1 — π(x)) + π(x).

Стоит отметить, что вероятности перехода не зависят от свежести ссылок и пользователь выбирает старые и новые ссылки с одинаковой вероятностью. По этой причине мы освежаем вероятности перехода путём взвешивания ссылок в соответствии с оценкой новизны страниц перехода. В следующем разделе мы описываем измерение этой новизны.

4. Fresh BrowseRank
Определим меру новизны страницы. Мы используем фреймворк из работы [16]. Рассмотрим два момента времени τ, Т, τ < Т. Мы разделяем интервал [τ,Т] на К частей: [ti-1,ti], i ∈ {1,2,…,K}, t0 = τ, ti-ti-1 = (T — τ)/k. Для каждой страницы p из V определим через t(p) дату создания. Мы считаем, что вершина x была создана в момент времени τ.
Пусть i ∈ {1,2,…,K}. Пусть p ∈ V — это вершина, созданная до ti. Мы определяем оценку новизны Fi(p) p в i-ом интервале времени следующим образом:
1) Мы определяем начальное значение Fi0(p) забирая новизну страницы p и её ссылок как (27):

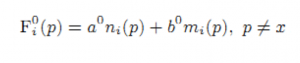где a0, b0 — неотрицательные параметры; ni(p) = 1 если вершина p создана в i-ом периоде, иначе ni(p) = 0; mi(p) — это число посещений страницы в i-ом периоде. Устанавливаем Fi0(x) = 0.

2) Начальная оценка Fi0(o) распределяется по вершинам через исходящие рёбра (28):

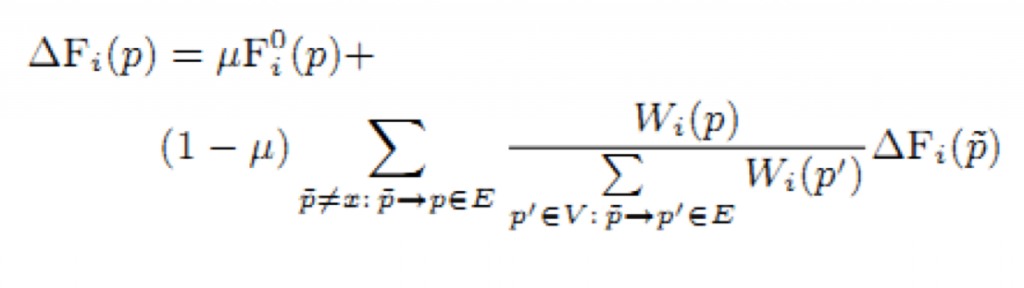где μ ∈ [0,1], Wi(p) — это оценка, назначенная «локальной» мерой новизны вершине p в i-ом периоде времени. Эта мера определяется таким же образом, как начальная мера Fi0 (значения параметров могут отличаться от параметров в уравнении (27)) (29),

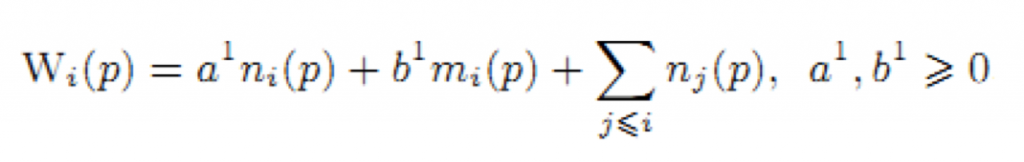Мы хотим «распространить меру новизны» по исходящим со страницы ссылкам, даже если среди них нет свежих ссылок. Поэтому мы увеличиваем вес страницы на 1 (последнее слагаемое в формуле 29), если она была создана до времени ti. Система, описанная в уравнении 28 иллюстрирует влияние соседей на меру новизны страницы.

3) Наконец, мера новизны Fi определяется как Fi(p) = ΒFi-1(p) + ΔFi(p). Мера экспоненциально уменьшается со временем, если нет никакой активности у вершины p (параметр Β из (0, 1)). В действительности Fi(p) = ΒiΔF0(p) если не было активности за период [τ, ti].
В уравнении 28 все рассматриваемые вершины и рёбра созданы до момента времени ti.
Пусть мера новизны назначит странице p в графе G оценку Fk(p). Мы освежаем вероятность перехода путём замены I(p1,p2) на I(p1,p2)Fk(p2). Другими словами вероятность свежего перехода wf(p1→p2) ребра p1→p2 равно I(p1,p2)Fk(p2)/(∑p:p1→p∈EI(p1,p)FK(p)) и Fresh BrowseRank p равен Q(p)πF(p), где

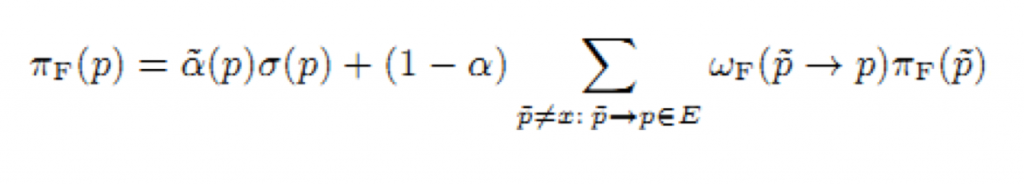В таблице 1 представлено описание всех параметров алгоритма.
Таблица 1. Параметры Fresh BrowseRank.

 

5. Обучение
Пусть fq(p) — значение нашей характеристики страницы p и запроса q. Сделаем её запросо-зависимой путём линейной комбинации Fresh BrowseRank с запросо-зависимой характеристикой.
Обучающая выборка содержит коллекцию запросов и наборы страниц Vq1, Vq2,…,Vqk для каждого запроса q, которые отсортированы от наиболее релевантных (свежих) к нерелевантным страницам. Другими словами Vq1 — это набор всех страниц с самой высокой оценкой. Для любых двух страниц p1 ∈ Vqi, p2 ∈ Vqj пусть h(i,j,fq(p2) — fq(p1)) будет значением пенальти, если позиция страницы p1 в соответствии с нашим алгоритмом ранжирования выше, чем позиция страницы p2 но i < j. Функция h — это функция потери (loss function). Мы рассматриваем потери с границами bij > 0, где 1 ≤ i < j ≤ k: h(i,j,x) = max {x + bij, 0}2. Пусть w — это вектор параметров Fresh BrowseRank.

Минимизируем вектор методом градиентной оптимизации. Алгоритм ранжирования новизны требует частой настройки параметров. Простой выбор значений параметров из крупной выборки отнимает много времени. Поэтому применение простой оценки существенно снизит качество поисковой выдачи. Покажем, как мы нашли производную дπF/дwi. Насколько нам известно, мы первые получившие производные от стационарного распределения процесса Маркова когда его вероятности перехода — это функции стационарного распределения другого процесса Маркова (вложенные процессы Маркова широко применяются, см. [15], [16]). Легко найти производные дπFresh/дα через решение следующей системы линейных уравнений (30), (31).

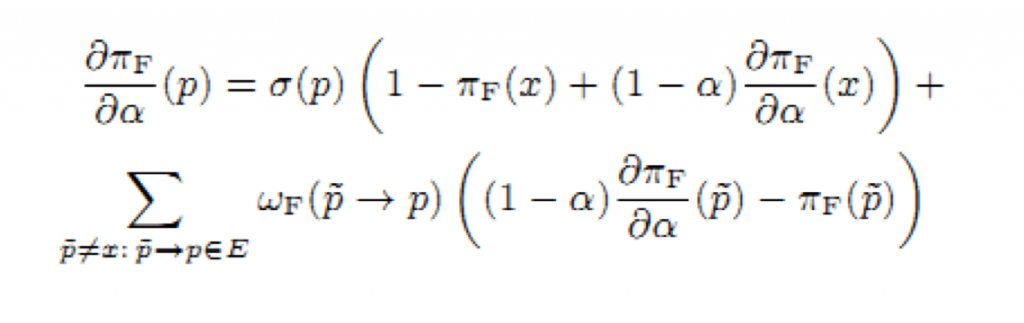
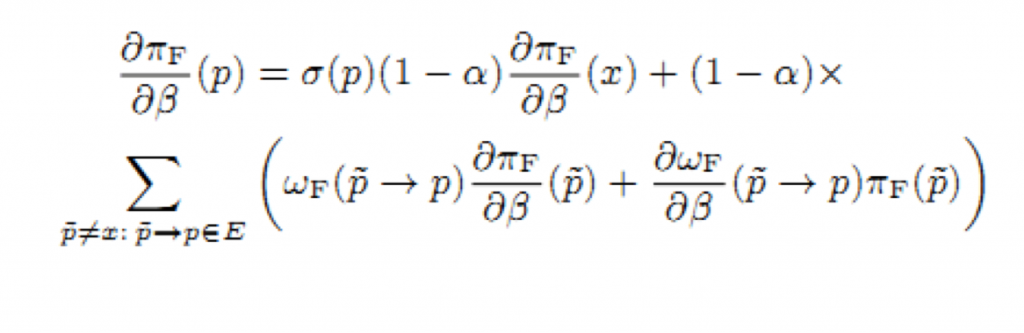получаем производную дw/дΒ(q→p) через нахождение дFk/дΒ(p) из уравнения:

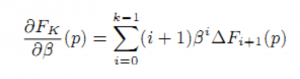Представим системы линейных уравнений с решениями дπF/дμ, дπF/дα0, дπF/дα1 (производные дπF/дb0, дπF/дb0 — решения тех же уравнений). Первые уравнения системы аналогичны уравнениям из (5). Нам только требуется выбрать рассматриваемый параметр вместо Β. Остаётся найти дΔFi/дμ, дΔFi/дα0, дΔFi/дα1:

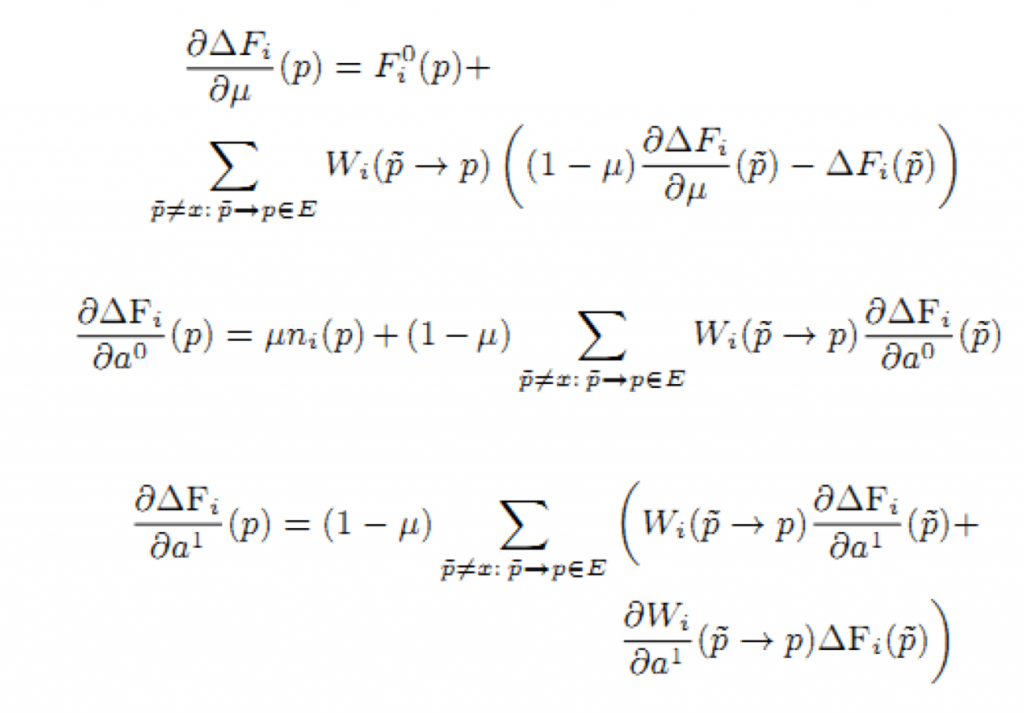параметры τ, Т, К выбираются из небольшого числа вариантов. Мы рассматриваем интервал времени [τ,Т] длиной в 1 неделю. Параметр К выбирается таким образом, чтобы длина одного периода [ti-1,ti] были либо 1 день, либо 6 часов, 3 часа и 1 час.

6. Результаты эксперимента
Все эксперименты проводились на страницах и ссылках сканированных в декабре 2012 популярной коммерческой поисковой системой. Мы использовали все данные с тулбаров с 10 декабря по 16 декабря 2012. В выборке было 113 млн. страниц и 478 млн. переходов. Для оценки ранжирования мы выбрали ряд запросов, поданных реальными пользователями за период с 14 по 17 декабря. Запрос — это пара «текст запроса, время запроса». Каждый запрос был оценён экспертами, нанятыми поисковой системой. Когда ассессор оценивал пару «запрос, URL», он назначал оценку и новизне страницы в соответствии с временем запроса и оценивал тематическую релевантность страницы запросу. Из-за специфики задания мы рассматривали только чувствительные к новизне запросы, на которые и нацелен наш алгоритм. Чтобы иметь должную релевантность для таких запросов, документы должны были быть и новыми и отвечающими тематике одновременно. Ассессоры были проинструктированы оценивать документы как новые, если тулбар делал запись не раньше 3 дней до момента оценки. Наконец, вышеописанные процедуры вылились в 200 оцененных запросов по новизне и 3000 пар запрос-URL.

Оценка релевантности проводилась по пятибалльной шкале: Идеально, Отлично, Хорошо, Неплохо, Плохо. Мы разделили данные на две части. На первой части (75% данных) мы обучали параметры, а на второй тестировали работу алгоритма. Мы сравнили Fresh BrowseRank с классическим BrowseRank так же, как это делали Dai и Davison [15] и Жуковский [16]. Алгоритмы были линейно скомбинированы по рангам при помощи BM25. Затем параметры Fresh BrowseRank выбирались путём максимизации функции потери. Параметр линейной комбинации BM25 выбирался через максимизацию метрики NDCG. Мы получили следующие параметры:

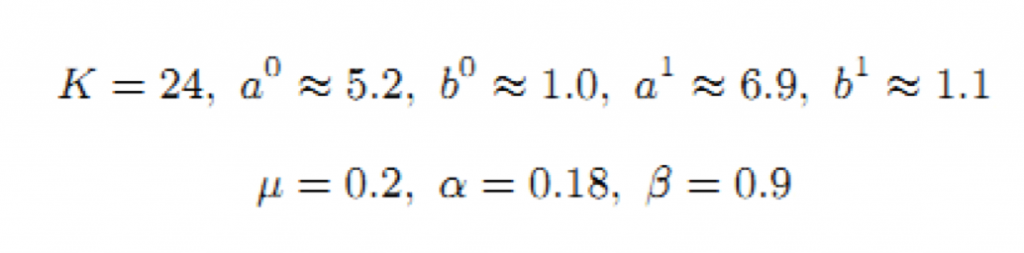Параметр K выбирался из набора {7, 28, 56, 168}. В этих случаях длины интервалов [ti-1,ti] равнялись 1 дню, 6 часам, 3 часам и 1 часу, соответственно.
Таблица 2 демонстрирует производительность алгоритмов по метрикам NDCG@5 и NDCG@10.

Таблица 2. Производительность.

7. Заключение
В данной работе мы представили Fresh BrowseRank, следующий алгоритм анализа пользовательского поведения, чувствительный к новизне. Мы сравнили его с классическим BrowseRank. Наш алгоритм был протестирован на крупном объёме данных и продемонстрировал превосходство над BrowseRank. Кроме непосредственного интереса наших результатов, они так же могут быть полезны коммерческим поисковым системам, желающим улучшить качество своей выдачи. Естественно, стоит предлагать и другие алгоритмы анализа пользовательского поведения, чувствительные к новизне, на основе нашего фреймворка. По этой причине мы считаем, что наш подход будет фундаментом исследований в данной области. Было бы интересно изучить прочие аспекты пользовательского поведения, однако нам не хватает алгоритмов. Например, стоит представить слой узлов запросов в виде графа. Так же мы представили методику обучения параметров вложенных процессов Маркова. Было бы интересно использовать эти алгоритмы для других алгоритмов, основанных на схожих процессах.

8. Ссылки
[1] Y. Liu, B. Gao, T.-Y. Liu, Y. Zhang, Z. Ma, S. He, H. Li, BrowseRank: Letting Web Users Vote for Page Importance. Proc. SIGIR’08, pp. 451-458 , 2008.
[2] L. Page, S. Brin, R. Motwani, and T. Winograd, The PageRank citation ranking: Bringing order to the web. dbpubs.stanford.edu/pub/1999-66, 1999.
[3] Y. Liu. T.-Y. Liu, B. Gao, Z. Ma, H. Li, A framework to compute page importance based on user behaviors, Inf Retrieval, 13: 22-45, 2010.
[4] B. Gao, T.-Y. Liu, Z. Ma, T. Wang, H. Li, A General Markov Framework for Page Importance Computation, Proc. CIKM’09, pp. 1835-1838, 2009.
[5] M. Eirinaki, M. Vazirgiannis, UPR: Usage-based Page Ranking for Web Personalization, Proc. on Fifth IEEE International Conference on Data Mining, pp. 130–137, 2005.
[6] Z. Gyongyi, H. Garcia-Molina, J. Pedersen, Combating web spam with trustrank, Proc. InVLDB’04, pp. 576-587, 2004.
[7] B. Gao, T.-Y. Liu, Yu. Liu, T. Wang, Z.-M. Ma, H. Li, Page Importance Computation Based on Markov Processes. Inf. Retrieval, 14 (5), pp. 488-514, 2011.
[8] G. Zhu, G. Mishne, Mining Rich Session Context to Improve Web Search, Proc. KDD’09, pp. 1037-1046 , 2009.
[9] Y. Liu, Y. Jin, M. Zhang, S. Ma, L. Ru, User Browsing Graph: Structure, Evolution and Application, WSDM 2009, 2009.
[10] P. S. Yu, X. Li, and B. Liu, On the temporal dimension of search. Proc. WWW’04, pp. 448-449, 2004.
[11] E. Amitay, D. Carmel, M. Herscovici, R. Lempel, and A. Soffer. Trend detection through temporal link analysis. Journal of the American Society for Information Science and Technology, 55(14), pp. 1270-1281, 2004.
[12] K. Berberich, S. Bedathur, M. Vazirgiannis, G. Weikum. Buzzrank… and the trend is your friend. Proc. WWW06, pp. 937-938, 2006.
[13] K. Berberich, M. Vazirgiannis, G. Weikum, Time-aware authority ranking. Int. Math., 2(3), pp. 301–332, 2005.
[14] L. Yang, L. Qi, Y. P. Zhao, B. Gao, and T. Y. Liu. Link analysis using time series of web graphs. Proc. CIKM’07, pp. 1011-1014, 2007.
[15] Na Dai and Brian D. Davison, Freshness Matters: In Flowers, Food, and Web Authority. Proc. SIGIR’10, pp. 114-121, 2010.
[16] M. Zhukovskii, D. Vinogradov, G. Gusev, P. Serdyukov, A. Raigorodkii, Recency-sensitive model of web page authority. Proc. CIKM’12, pp. 2627-2630, 2012.

Fresh BrowseRank
Алексей Толстиков, Михаил Шахрай, Глеб Гусев, Павел Сердюков
Yandex
Россия 199021 Москва, ул. Льва Толстого, 16
{zhukmax, akhropov, gleb57, pavser}@yandex-team.ru

Перевод текста был взят с сайта.

by Mr. Роман Морозов and & Ms. Наталья Чердак